Whether real or complex (Cubic Equation)

This post deal with the conditions to check whether the roots are real or complex of a cubic equation. A cubic equation always has a real root. The other two roots are real or complex according as the graph cuts the x axis in one or three positions. If the graph touches the x-axis then two roots are equal. If the graph cuts the x-axis in three positions then all the roots are real. If the graph cuts the x-axis in one position then other two roots are complex. When we look at the graph of a general cubic equation we see a cup like structure and a cap like structure. The base of the cup like structure gives local minima and the top of cap like structure gives local maxima. Let us find the positions where the curve bends and changes its direction. We call the cup like structure concave upward and a cap like structure convex upward. The quadratic equation is ax³ + bx² + cx + d = 0. Let it be equal to y or f(x). y = ax³ + bx² + cx + d. Now the rate of change of curve is f '(x) = 3ax² + 2bx + c. f(x) is differentiated to obtain f '(x). We again differentiate f '(x) to obtain f ''(x),

f ''(x) = 6ax + 2b
f ''(x) = 6a(x + b/3a)

Let us check, for what values of x it may give maxima and for what values it may give minima.
There are four cases for it and is given in the following table

f ''(x)	x	a	state
> 0	x < (−b/3a)	a < 0	minima
< 0	x > (−b/3a)	a < 0	maxima
< 0	x < (−b/3a)	a > 0	maxima
> 0	x > (−b/3a)	a > 0	minima

When the local maxima and and local minima are on opposite sides of x-axis then all the roots are real.

Let us find the x-coordinate of maxima or minima. It is when f '(x)=0.

Solving 3ax² + 2bx + c = 0 we get
x = [−2b±√(4b² − 12ac)]/6a
x = [−b±√(b² − 3ac)]/3a
or
x₁ = [−b+√(b² − 3ac)]/3a
and
x₂ = [−b−√(b² − 3ac)]/3a Find the value of y for x₁ and x₂, substituting them in place of x.

For x₁ we get y₁ = [4b³ − 15abc + 27a²d + (6ac − 2b²)√(b² −3ac)]/27a²

For x₂ we get y₂ = [4b³ − 15abc + 27a²d − (6ac − 2b²)√(b² −3ac)]/27a²

Now local maxima and local minima lie on the opposite sides of the x-axis when y₁ and y₂ lie on the opposite sides of x-axis. This will happen when they are of opposite sign.

Now four cases arise:

y1	y2	Remark
y1< 0	y2< 0	One root is real and other two are complex. Graph of  y = x3 + 4x2 + 4x − 7
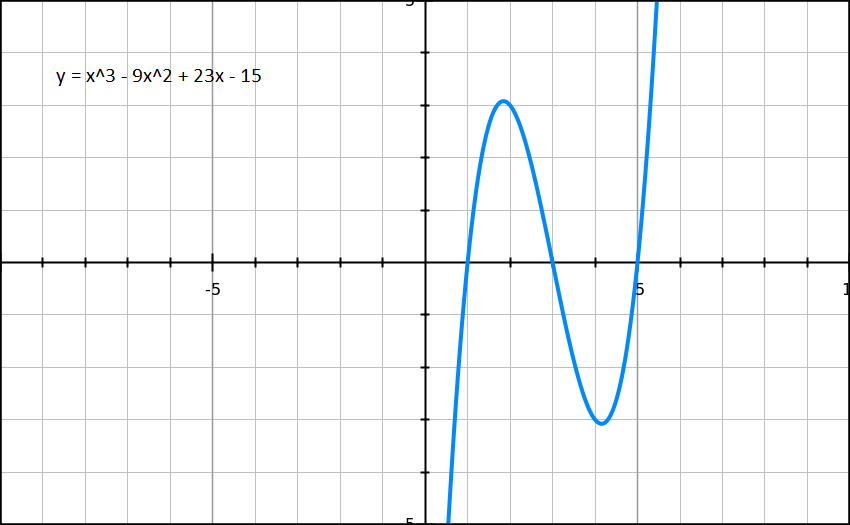
y1< 0	y2> 0	All the three roots are real.  Graph of y = x3 + 6x2 + 4x − 7 If y1 = 0 or y2 = 0 then there are two equal roots and it may be   [−b+√(b2 − 3ac)]/3a or [−b-√(b2 − 3ac)]/3a
y1> 0	y2< 0	All the three roots are real. Graph of y = − x3 + 4x2 + 4x − 7 If y1 = 0 or y2 = 0 then there are two equal roots. and it may be   [−b+√(b2 − 3ac)]/3a or [−b-√(b2 − 3ac)]/3a
y1> 0	y2> 0	One root is real and other two are complex. Graph of y = x3 + 4x2 + 4x + 7

When (b² − 3ac) is less than zero then y₁ and y₂ are complex and there is no maxima and minima. Then the equation has only one real root and other two are complex. See the graph for 3x² + 2x² + 3x + 4 = 0.
Where (b² − 3ac) = (4 − 27) < 0.

When y₁ or y₂ is equal to zero then there are two equal roots.

Whether real or complex (Quadratic Equation)

This post deals with the conditions to check whether the roots are real or complex. The roots are real when the graph really cuts the x-axis. When we look at the graph of a quadratic equation we see a cup like structure or cap like structure. Let us check when it is cup like and cap like. We call the cup like structure concave upward and a cap like structure convex upward. The quadratic equation is ax² + bx + c = 0. Let it be equal to y or f(x). Now the rate of change of curve is f'(x) = 2ax + b. f(x) is differentiated to obtain f'(x). We again differentiate f'(x) to obtain f''(x), f''(x) = 2a. Now we find the x-coordinate of the point where the slope is zero i.e. f'(x) = 0.

2ax₁ + b = 0
⇒ x₁ = −b/2aNow the point on the graph is concave upward or convex upward according as the point at the x-coordinate x₁ = −b/2a is maxima or minima. This thing is determined by checking the value of f''(x). If it is positive then the curve has minima and if it is negative then the curve is maxima. We have f''(x) = 2a. It is positive if a is positive and negative when a is negative. Hence we can make following conclusions

1. concave : The graph is concave upward if a is positive.
   
   
   
   The graph given above is of the function f(x) = 2x² + 4x - 3.


2. convex : The graph is convex upward if a is negative.
   
   
   The graph given above is of the function f(x) = −2x² + 4x + 3

Now, we find the y coordinate of the point where it moves upward or downward traveling from x = −∞ at x = -b/2a. It changes its direction at −b/2a to opposite direction of y-axis.
y = ax² + bx + c
at x = x₁ = −b/2a
y₁ = a(−b/2a)² + b(−b/2a) + c
= b²/4a − b²/2a + c
= − b²/4a + c
= − (b² − 4ac)/4a

Now, four conditions arise as given in the following table

a	b2−4ac	Comment
−ve	−ve	The value of y1 is −ve and the curve is concave downward. The curve will be present below y1. Hence it will cut the x-axis at no points. So the roots are imaginary.
−ve	+ve	The value of y1 is +ve and the curve is concave downward. The curve will be present below y1. Hence it will cut the x-axis at one or two points. So the roots are real and may be equal if y1 = 0.
+ve	−ve	The value of y1 is +ve and the curve is concave upward. The curve will be present above y1. Hence it will cut the x-axis at no points. So the roots are imaginary.
+ve	+ve	The value of y1 is −ve and the curve is concave upward. The curve will be present above y1. Hence it will cut the x-axis at one or two points. So the roots are real and may be equal if  y1 = 0.

Quadratic equation

A quadratic expression when equated to zero is called a quadratic equation. A quadratic equation looks like this ax² + bx + c = 0. In this post I will show you a method which is very good to find the solution of a quadratic equation. I found this method.Let us look at the method.

ax² + bx + c = 0

We can write it as,
(x + b/a)x + c/a = 0
or (x + b/a)x = -c/a

Let A = x + b/a and B = x
Then,A-B = b/a, AB = -c/a and A+B = 2x + b/a
Applying the identity (A+B)² = (A-B)² + 4AB
(2x + b/a)² = (b/a)² - 4c/a = (b² - 4ac)/a²
2x + b/a = ±(1/a)√(b² - 4ac)
x = (-b ± √(b² - 4ac))/2a

As we can see there are two values which satisfy the equation hence the number of solutions is two and there are two roots. As the solutions of a quadratic equation are called roots.

Let us analyze the roots i.e. when they are real. The value under the square root is positive if b² - 4ac is positive. When such condition arises then the roots are real. The value b² - 4ac is called the discriminant. If the discriminant is equal to zero then both the roots are equal. If the discriminant is negative then both the roots are imaginary and they occur in conjugate pairs. If the roots are real and distinct then the graph cuts the x-axis at two different points. If the roots are real and equal then the graph cuts the x-axis at one point. If the roots are imaginary then the graph does not cut the x-axis.

The graph below shows two real roots.
x² + 5x - 2 = 0

The graph below shows two real roots
x² + 5x + 6.25 = 0

The graph below represents when roots are imaginary.

x² + 5x + 8 = 0

Solution is a solution

Let us start with two equations

1. ax + b = 0
2. ax² + bx + c = 0

Among the above two equations one is linear and the other is quadratic. The solution of the linear equation is x = -b/a and the solution of the quadratic is (1/2a)(-b±√(b² - 4ac)). The point which I want to state is that the solution of a quadratic equation contains the solution of a linear equation. When we substitute c for zero in the quadratic equation then we get ax² + bx = 0. On factorizing we get (ax + b) = 0 and x = 0. Whose solutions are x = -b/a and 0. -b/a is the solution of ax + b = 0. And x = 0 comes because x is multiplied throughout to get the equation ax² + bx = 0.

Now according to me if solution of cubic exist then it must have the solution of quadratic contained in it. Similar is the case for the others. Let us compute the solution of a cubic equation when one root is known

The equation is ax³ + bx² + cx + d =0. If the roots are α, β and γ and γ is known then
α + β + γ = -b/a
αβ + βγ + γα = c/a
αβγ = -d/a
Expressing sum of two roots in terms of third
α + β = -b/a - γ
Expressing product of two roots in terms of third
αβ = c/a - (βγ + γα)
αβ = c/a - γ(β + α)
αβ = c/a - γ(-γ - b/a)
αβ = c/a + γ² + bγ/a
(α - β)² = (α + β)² - 4αβ
(α - β)² = (-b/a - γ)² - 4(c/a + γ² + bγ/a)
(α - β)² = (-b/a)² + (γ)² + 2bγ/a - 4c/a - 4γ² - 4bγ/a
(α - β)² = b²/a² - 4c/a - 3(γ)² - 2bγ/a
α - β = ±√[(b² - 4ac)/a² - 3(γ)² - 2bγ/a]
adding α - β and α + β
2α or 2β = -b/a - γ ± √[(b² - 4ac)/a² - 3(γ)² - 2bγ/a]
α or β = -b/2a - γ/2 ± (1/2a)√[(b² - 4ac) - 3a²(γ)² - 2baγ]

As we can see when one root γ = 0 and the equation is independent of d then the solution reduces to the solution of a quadratic equation.

Now it can be the solution of 5^th degree equation exist and it contains the solution of 4^th degree in it.

A cubic gives cubic

I ask you a question and the answer is very simple. But it has a very interesting conclusion in it. The question is "If we take a cubic equation and consider A as one number. Now If we find the difference of the roots from this point A and frame an equation which gives the values. What will we get."

The answer is very simple and is a cubic. The expression will be a cubic because we know that there are three roots and each value will be at a constant distance from the given number A. So there will be three numbers and a cubic equation only gives three values i.e. three numbers when equated to zero.

Now the question arises how can we find that equation. Suppose the equation is f(x) and the number is A. Then, the required equation is
f(x+δ) = f(x) + f'(x)δ /1!+ f''(x)(δ)² /2!+ f'''(x)(δ)³/3! +...

The above equation can be helpful for a cubic if we know one root.

Suppose the equation is f(x) = (x - 1)(x - 2)(x - 3)
= x³ - 6x² + 11x - 6

Now as 1 is a root then
f(1+δ) = f(1) + f'(1)δ/1! + f''(1)(δ)² /2!+ f'''(1)(δ)³/3!
f(1+δ) = f(1) + (3x² - 12x + 11)δ + (6x - 12)(δ)²/2 + 6(δ)³/6   x=1
f(1+δ) = 2δ - 3δ² + δ³
f(1+δ) = δ(2 - 3δ + δ²)
For the other roots f(1+δ) = 0 So,
Solving, δ(2 - 3δ + δ²) = 0
we get, δ = 0,1,2. Hence the roots are 1,2,3.

Solution of a cubic equation (Part 1)

In elementary algebra it is of prime interest to find the solution of a cubic equation.In this post and few other posts we will find the solution of a cubic equation. As from the previous post we know that the cubic is symmetric with respect to some x = a. In this post let us find the condition when the cubic expression has the middle point on line y=0 and what are the solutions of the corresponding cubic equation.

Let the cubic expression be y = ax³ + bx² + cx+ d.
Differentiating y w.r.t. x we get y' = 3ax² + 2bx + c. Here the sum of the slopes is −2b/3a. Now when we take a particular slope and put it in the equation of y' then we get a quadratic equation. We know that a quadratic equation has two roots. This implies that as the middle point of the curve has both the slopes equal as that point has a unique value. So slope is half of the value −2b/3a i.e. −b/3a. Which we have seen in the previous post. Now we have to find the value of x for which the slope is −b/3a. At this point we know that the difference between the slopes is zero as it has unique value so the rate of change of slope is zero. Differentiating again w.r.t. x we get y'' = 6ax + 2b. We find that the point where rate of change of slope is zero is -b/3a. Equating 6ax + 2b to 0. x has value −b/3a at the point where the rate of change of slope is zero.

Now we will find the value of y for this point. It is
y₁ = a(−b/3a)³ + b(−b/3a)² + c(−b/3a) + d
y₁ = −b³/(27a²) + b³/9a² − bc/3a + d
y₁ = 2b³/27a² − bc/3a + d
When this value is zero then the roots can be found very easily. In this case the center of the curve lies on the axis y = 0. I will tell what are the properties of the roots at the last.
when y₁ = 0 then d = bc/3a − 2b³/27a²

Now let us find the value of x where the slopes are zero. We get
3ax² + 2bx + c = 0
x = [−2b ± √(4b² − 12ac)]/6a
x = [−b ± √(b² − 3ac)]/3a
x₁ = [−b − √(b² − 3ac)]/3a
x₂ = [−b + √(b² − 3ac)]/3a
The center root lies at the middle of the points where the slopes are zero.
So,if δ is the distance of the middle root from the points where the slopes are zero then x₁ + δ = x₂ − δ.
δ = (x₂ − x₁)/2
δ = [√(b² − 3ac)]/3a
Hence the middle root is β = −b/3a.
Let the other roots be at a distance p from the middle root. Then
(β − p)(β + p)β = −d/a
(β − p)(β + p)β =− [bc/3a − 2b³/27a²]/a
(β − p)(β + p) = − [bc/3a − 2b³/27a²]/aβ
(β² − p²) = [bc/3a − 2b³/27a²]3/b
(β² − p²) = [c/a − 2b²/9a²]
(β² − p²) = [9ac − 2b²]/9a²
p² = β² + [2b²−9ac]/9a²
p² = b²/9a² + [2b² − 9ac]/9a²
p² = [3b² − 9ac]/9a²
p = ±√[3b² − 9ac]/3a
Hence the roots are
α = { − b − √[3b² − 9ac]}/3a;
β = −b/3a;
γ = { − b + √[3b² − 9ac]}/3a

Properties of the roots

The outer roots are equidistant form the middle root.

The roots are
α = { −b − √[3b² − 9ac]}/3a;
β = −b/3a;
γ = { − b + √[3b² − 9ac]}/3a
if the equation ax³ + bx² + cx + d = 0
satisfies d = bc/3a − 2b³/27a²

Solution of Quadratic by graph

The solution of a quadratic equation, cubic equation is possible with graph. I have found a method by which we can find the solution of a quadratic, cubic, etc, equations with the help of graph when one of the solution is known. The solution consists of finding a equation which relates the roots of the equation. It is very easy to find such a solution. Although the equation consists of only two roots but when we examine the roots then we can find all the roots of the equation. We will find the expression for quadratic equation in this post and discuss cubic equation in the next post. The method goes like this.

1. Let the equation be ax² + bx + c = 0
2. Take two roots of the equation. Let it be x₁ and x₂.
3. Form one equation with one root.
   ax₁² + bx₁ + c = 0 ---(i)
   Form one more equation with other root.
   ax₂² + bx₂ + c = 0 ---(ii)
   
4. Subtract (ii) from (i) and solve it
   (ax₁² − ax₂²) + (bx₁ − bx₂) + c − c = 0
   a(x₁² − x₂²) + b(x₁ − x₂) = 0
   (x₁ − x₂)[a(x₁ + x₂) + b] = 0
   Suppose both the roots are different, then
   [a(x₁ + x₂) + b] = 0
   (x₁ + x₂) = −b/a
   
You will get a relation in the roots.
5. Plot the relation on a graph by taking x₁ to be y and x₂ to be x.
   The relation becomes y = −x − (b/a)

Graphic Solution of two quadratic expressions y = x² + 5x + 6 and y = x² − 5x + 6 and their respective relation equation between roots are given. The roots can be found by checking where the quadratic graph cuts the x-axis.

The two straight lines gives the solution of the equations x² + 5x + c₁ = 0 and
x² − 5x + c₂ = 0. If we know one root of the equation then we can find the other root by looking at the point's corresponding coordinate point where one coordinate is equal. For example as one roots of x² + 5x + 6 = 0 is 2 so the corresponding point on the curve taking x = 2 is (2,3) so the other root is 3. We can also find the roots by looking at the point (a,b) where the area formed by the rectangle between x-axis, y-axis, x = a and y = b have area equal to the constant term. The condition for the roots for a particular equation is that the roots has product equal to c/a, where c is the constant term and a is coefficient of x².

Solution of a Cubic by graph

As we have seen in the post 'Solution of Quadratic by Graph' we can represent solution of a quadratic equation. Similarly we can represent solution of a cubic equation also by graph. The method is the same we represent a relation between two roots. The relation gives us a graph which has solution as the value of x coordinate and the corresponding y coordinate. In the case of cubic we get an ellipse. Let us first find the relation between two roots of a cubic equation.

1. Let the equation be ax³ + bx² + cx + d = 0
2. Take two roots of the equation. Let it be x₁ and x₂.
3. Form one equation with one root.
   ax₁³ + bx₁² + cx₁ + d = 0 ---(i)
   Form one more equation with other root.
   ax₂³ + bx₂² + cx₂ + d = 0 ---(i)
   
4. Subtract (ii) from (i) and solve it
   (ax₁³ − ax₂³) + (bx₁² − bx₂²) + (cx₁ − cx₂) + d − d = 0
   a(x₁³ − x₂³) + b(x₁² − x₂²) + c(x₁ − x₂) = 0
   (x₁ − x₂)[a(x₁² + x₂² + x₁x₂) + b(x₁ + x₂) + c] = 0
   Suppose both the roots are different, then
   [ax₁² + ax₂² + ax₁x₂ + bx₁ + bx₂ + c] = 0
   [ax₁² + ax₁x₂ + bx₁ + ax₂² + bx₂ + c] = 0
   [ax₁² + x₁(ax₂ + b) + (ax₂² + bx₂ + c)] = 0
   solving in x₁ we get,
   x₁ = (1/2a)( − (ax₂ + b)±√((ax₂ + b)² − 4a(ax₂² + bx₂ + c)))
   x₁ = (1/2a)( − (ax₂ + b)±√(−3a²x₂² − 2abx₂ + b² − 4ac))
   
You will get a relation in the roots.
5. Plot the relation on a graph by taking x₁ to be y and x₂ to be x.
   The relation becomes y = (1/2a)( − (ax + b)±√( − 3a²x² − 2abx + b² − 4ac))
   Divide the relation into two parts one with + sign and other with − sign. Plot them.

Solution of the cubic equation in the above graph is 1,2 and 3. As we can see from the graph that the solution exist where the line x=1 or x=2 or x=3 cuts the curve. When we look at the line x = 1, then we find that the line cuts the curve at y=2 and y=3. Similarly we see that the curve is cut by the line x=2 at y=1 and y=3. So is the case with x=3, where y=1 and y=2. So the solutions of the equation is the points satisfying the condition that the product of the roots is equal to the negative of the constant term divided by coefficient of x³.

Similarly on the guidelines for the previous graph we find that the solution is 1,2 and 4.

When the graph is plotted then the roots of the family of curves ax³ + bx² + cx + k = 0, where k is parameter is given by the curve which is like the ellipse. If one root is known to be α. Then other two roots can be found by looking at the points where the line x = α intersect the ellipse. By noting down the two values of y where the line x = α intersect we get the three roots. The two values of y and one value of x or two values of x and one value of y are the three roots of the curve.